animation, comics, exhibits, events, etc!

On alternating Fridays, Michael Carlisle examines the world “outside” sequential art to find… more sequential art. Expect mathematics and a dash of pessimistic optimism.

In my first post, I posited that math is a sequential art. I’d like to expand on my comment, making a semi-counterpoint to this post.

Mathematics is certainly a sequential art, but math is not comics.

Math can be done completely in words, without images or even symbols outside a written language’s letters and numbers; specialized symbols and pictures are used almost universally to aid in the understanding. It should be pretty easy to see that without these specialized symbols and illustrations, written math would be nigh-unreadable, but it is possible.

While understanding is strongly desired, some hardcore Platonists would probably have you believe that your comprehension is not necessary for math’s existence. As there may be an “ideal chair” or “ideal pizza” from which all chairs and pizzas gain their physical characteristics, your suboptimal, barely-adequate chair and pizza, as just an example of these ideals, give you the idea of them without giving you full access to PIZZANESS or CHAIRNESS.

Likewise with proofs and pictures. Sometimes, pictures just don’t work – they can’t possibly give you PROOFNESS¹ for a given problem. Like whenever you need to show something that happens in an infinitely-varying structure. Say you’re looking at a fractal. I know, I know, most commonly-used “math image,” but the whole point of looking at a fractal is that you can’t really see all the detail. If you zoom in, it looks the same, no matter how far you go.

As an example, I’ll give a theorem whose understanding is greatly aided by images, but cannot possibly be proven by them.

Brouwer’s Fixed Point Theorem states:

Every continuous function of a closed n-dimensional ball to itself has a fixed point – a point with .²

You would think that something like a fixed point theorem, where the proof requires you to show that something that can (often) be drawn stays in the same place would be easily proven with a picture. Nope.

First issue: we can actually show it for an easy-to-draw function in one dimension – – with a picture, but the proof for all cases uses the intermediate value theorem. Still, it’s easy enough with just a little calculus.

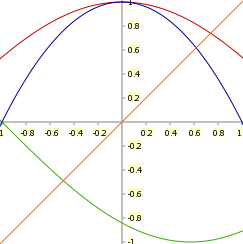
Graph, courtesy CALC5. Showing that a function has a fixed point is as easy as noticing that it intersects with the line , in yellow. Note that this is NOT a proof, just a few examples.

Next, you can’t really draw things in higher than two dimensions that easily or at all. Oh well.

Third, we need proof. That means all cases, not just a couple that look pretty in picture form. That almost definitely takes words.

To prove Brouwer’s theorem in two or more dimensions, we’ll go to what is by some considered to be the Platonic ideal: Proofs from THE BOOK, based on Paul Erdös’ idea that God has a book of “perfect” proofs for certain big theorems. This book is a human attempt to select proofs they believe might be in this book.

I won’t prove all of it here, but I will give a crucial portion of the proof in two dimensions which switches from continuous-land into a more discrete setting (which is easier to picture) – Sperner’s Lemma. This is a combinatorial graph theory result that says:

Sperner’s Lemma: Suppose a “big” triangle is triangulated (that is, broken up into a bunch of smaller triangles). Assume the vertices of all the triangles are colored with three colors (say, red, blue, and green) with the “big” triangle’s vertices colored one each, and on the outer edges, only the colors between those outer points are used. (The “big” triangle has tricolored vertices, and, for example, the vertices on the outer edge between the outer red and blue vertices also only have red and blue.) Then there must be a “small” triangle with tricolored vertices.

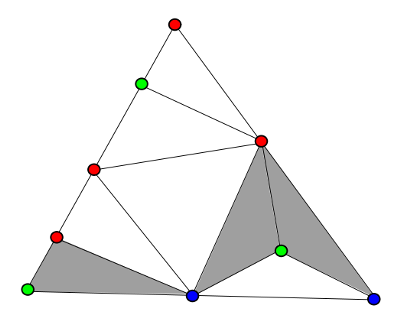
Sperner’s Lemma example, courtesy Wikimedia Commons. The tricolored triangles are shaded.

Since this is already known to be true, any example you draw (like the image above) will definitely come out with a tricolored small triangle. You cannot come up with a counterexample, but no matter how many different examples you draw out to convince yourself of this fact, your compiled drawings cannot constitute a proof of the theorem.³

(We can use Sperner’s Lemma because the closed disc can be deformed into a triangle. I won’t explain this, but it should be intuitive enough.) Sperner’s Lemma is proven combinatorially not by showing that such a tricolored small triangle exists, but that an odd number of such triangles exist. Clearly, then, at least one exists.

When you have a graph like this (a planar graph, where no edges cross), you can draw a dual graph which puts vertices in the faces of the existing graph and edges between vertices if the faces share an edge. We’ll draw a partial dual graph on our hypothetical vertex-colored graph, which only has dual edges crossing red-blue edges.

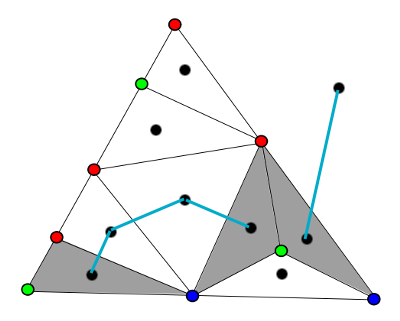
The partial dual graph to our example triangulation where the only edges we have are the ones crossing red-blue edges of the original graph. There is a dual vertex corresponding to “outside” – this is important in the proof of Sperner’s Lemma.

The degree of a vertex is defined as how many edges are attached to it. A vertex on the dual graph can have degree 0, 1, 2: 0 if it doesn’t have a red or doesn’t have a blue, 1 if it has one red and one blue, and 2 if it has 2 red and 1 blue or 2 blue and 1 red. (It can’t have 3 – why?) You should notice that a dual vertex will have degree 1 if and only if its triangle has tricolored vertices – one red-blue edge has a dual edge through it, and the other two don’t, which means that the third vertex must be green. We have some in our example, but it’s just an example; it doesn’t represent ALL cases.

On the outer edge between red and blue, we switch between red and blue. Since we start at red and end at blue, there must be an odd number of edges that have one red and one blue⁴ vertex, and hence there are an odd number of dual edges going through the outer edge. Since the number of odd-degree vertices in any graph (including our partial dual) is odd (so that the sum of all the degrees is even – think about why), then there must be an odd number of dual vertices with odd degree. But the only odd degree possible is 1, which means there are an odd number of 1-degree dual vertices. Therefore, there are an odd number of tricolored triangles, which means at least one.

To prove Brouwer’s theorem, we make a sequence (there’s that word again) of finer- and finer-grained tricolored triangulations, and since there is always a small tricolored triangle inside a bigger one (just triangulate inside it), we can limit to a point that’s fixed in a special way. Where it is we don’t know, just that it exists.

The images we’ve shown here are just an example, as they clearly display that the lemma is true in their particular case, not in general. You can’t claim the pictures help in the proof itself, only the understanding of it.

So, it depends on whether or not, for the sake of mathematical proof, you are a Platonist or not. If a proof exists (which, by Gödel, we can’t guarantee), is there an IDEAL PROOF? Does it matter if we understand it? Is mathematics the proof or the understanding? If you’re Brouwer, an intuitionist like Kronecker, who hated Cantor’s results, you think both: proofs should be intuitively understandable, using constructions showing the existence of what you want to find. In that sense, Brouwer would like this proof.

Do the images help in the intution? Definitely. Are they necessary? No – the text of the proof above could be used alone and still be understandable, albeit a bit less. In addition, certain images could be misleading; you might believe that all cases look like this one. They certainly don’t.

Now, if you’ll excuse me, I have experienced a construction of the existence of hunger, so I will go contemplate the aspects of PIZZANESS.

[1] That is, for direct, constructive proofs. If what you need to prove is a counterexample, then one picture might actually be all you need.

[2] If you want details, they’re easily available. I’ve linked throughout. I love the Internet.

[3] Compare this with the once-controversial computer-generated proof of the Four Color Theorem, which claims to exhaustively check all of its possible drawings.

[4] This is actually the very short proof of a discrete version of the Intermediate Value Theorem.

Michael Carlisle is a mathematics Ph.D. candidate at the City University of New York’s Graduate School and University Center (”Graduate Center”), where he earned a certificate in Interactive Technology and Pedagogy. When not teaching or researching probability or rambling about dystopian films and surrealist animation, he volunteers with the Sequential Art Collective and New York Center for Independent Publishing. He has more data than you.